6. Equilibrium Payoff Correspondence¶
In State Space we constructed a partition of the simplex 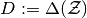 . Now, we let
. Now, we let 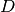 be the domain of the equilibrium payoff correspondence.
The task ahead is to approximate the equilibrium value correspondence
be the domain of the equilibrium payoff correspondence.
The task ahead is to approximate the equilibrium value correspondence 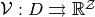 using
convex-valued step correspondences.
using
convex-valued step correspondences.
6.1. Background¶
Notation reminder:
Action profile of small players on
![[0,1]](_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) ,
, 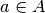 . (Assume
. (Assume 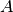 is a
finite set.) Each small player takes on a personal state
is a
finite set.) Each small player takes on a personal state 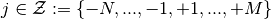 at each date
at each date 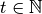 .
.Actions of large player (
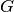 ),
), 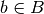 .
. 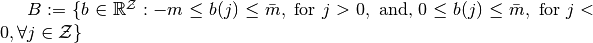 is a
finite set and contains vectors
is a
finite set and contains vectors 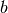 that are physically feasible
(but not necessarily government-budget feasible in all states).
that are physically feasible
(but not necessarily government-budget feasible in all states).Extended payoff vector space,
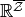 ,
where
,
where 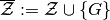 .
.Probability distribution of small players on finite set
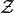 ,
, 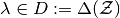 .
.Profile of continuation values of agents,
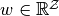 .
.Transition probability matrix at action profile
 ,
, 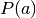
Individual
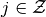 , given action
, given action 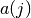 faces transition probability distribution,
faces transition probability distribution, 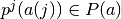
Flow payoff profile,
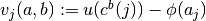 , where
, where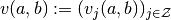 ;
;- Utility-of-consumption function,
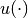 ; and
; and - Disutility-of-effort/action function,
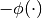 .
.
Public date-
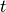 history,
history, 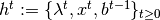 , where
, where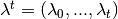 is a history of agent
distributions up to and include that of date
is a history of agent
distributions up to and include that of date 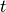 ;
;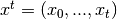 where
where 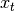 is a date-
is a date-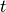 realization of the
random variable
realization of the
random variable ![X_t \sim_{i.i.d.} \mathbf{U}([0,1])](_images/math/9cd83d866a9bf2c16e7ac1983013000df4b7fdbe.png) ; and
; and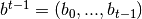 is a history of government policy
actions up to the end of date
is a history of government policy
actions up to the end of date 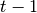 and let
and let 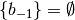 .
.
Also,
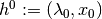 .
.
Definition (Consistency)
Let 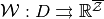 be a compact- and convex-valued correspondence having the property that
be a compact- and convex-valued correspondence having the property that 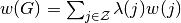 for all
for all 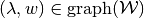 . A vector
. A vector 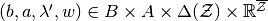 is consistent with respect to
is consistent with respect to 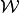 at
at 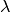 if
if
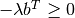 ;
;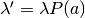 ;
;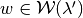 ; and
; and- For all
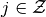 ,
, ![a(j)\in\text{argmax}_{a'}\left\{(1-\delta) \left[u(c^b(j))-\phi(a')\right]+\delta\mathbb{E}_{p^j(a')}[w(i)]\right \}](_images/math/a646fa966ddf25a8b2bc210b8281dea29cd2881e.png) .
.
Definition (Admissibility)
- For
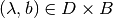 let
let ![\pi(\lambda,b):=\min_{(a',\lambda'',w')}
\left[(1-\delta)\sum_{j\in\mathcal{Z}}\lambda(j)[u(c^b(j))-\phi(a'(j))]
+ \delta\sum_{j\in\mathcal{Z}}\lambda''(j)w'(j)\right],](_images/math/f8e71d573a03d84b9369db8eabe2dd38deb43b6c.png)
subject to 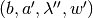 is consistent with respect to
is consistent with respect to 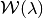 . Let
. Let 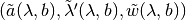 denote the solutions to the corresponding minimization problem. A vector
denote the solutions to the corresponding minimization problem. A vector 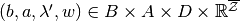 is said to be admissible with respect to
is said to be admissible with respect to 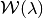 if
if
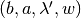 is consistent with respect to
is consistent with respect to 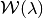 ; and
; and![(1-\delta)\sum_{j\in\mathcal{Z}}\lambda(j)[u(c^b(j))-\phi(a(j))]\delta\sum_{j\in\mathcal{Z}}\lambda'(j)w(j)\geq \max_{b'\in B(\lambda)}\pi(\lambda,b')](_images/math/27e692164fdc4c55c83bc2faa71f3b0c2fbf15af.png) , where
, where 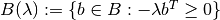 .
.
Admissible payoff vectors
The payoff vector defined by an admissible vector 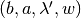 at
at 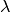 is given by
is given by
![E_G(b,a,\lambda',w)(\lambda)&=(1-\delta)\sum_{j\in\mathcal{Z}}\lambda(j)[u(c^b(j))-\phi(a(j))]+ \delta\sum_{j\in\mathcal{Z}}\lambda'(j)w(j)
\\
E_j(b,a,\lambda',w)(\lambda)&=(1-\delta) \left[u(c^b(j))-\phi(a(j))\right] + \delta \mathbb{E}_{p^j(a(j))}[w(i)].](_images/math/b1c2bf8ec4e4adb5c7ec21288d300a946ca510b8.png)
Note that 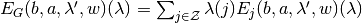 .
.
In the paper, we proved the following:
SSE Recursive Operator
A SSE is a strategy profile 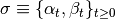 such that given initial game state
such that given initial game state 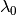 , for all dates
, for all dates 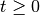 , and all public histories
, and all public histories 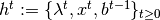 ,
, 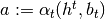 and
and 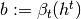 , and, if
, and, if 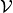 is the SSE payoff correspondence, then
is the SSE payoff correspondence, then 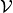 is the largest fixed point that satisfies the recursive operator
is the largest fixed point that satisfies the recursive operator
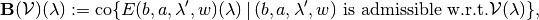
where 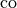 denotes the convex hull of a set.
denotes the convex hull of a set.
The object of interest can be found recursively: 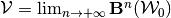 , for any initial
convex-valued and compact correspondence
, for any initial
convex-valued and compact correspondence 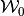 .
.
Note
Given state 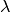 and agent payoff vector
and agent payoff vector
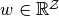 determine a unique corresponding
government payoff given by
determine a unique corresponding
government payoff given by 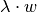 . We can thus ignore the
government payoff when defining the equilibrium value correspondences and
their approximations, and restrict their codomain to
. We can thus ignore the
government payoff when defining the equilibrium value correspondences and
their approximations, and restrict their codomain to
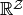 .
.