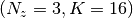1. State Space¶
Consider the game state space as 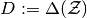 , the set of
all probability measures on the finite individual state-space
, the set of
all probability measures on the finite individual state-space
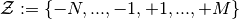 , where
, where 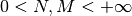 .
Let
.
Let 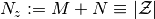 .
.
1.1. Properties¶
The set 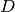 is:
is:
- is a unit simplex embedded in
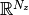 :
:
![\begin{equation*}
\Delta (\mathcal{Z}) := \left\{ \lambda \in \mathbb{R}^{N_{z}}:
\lambda_{i} \in [0,1], \forall i = 1,...,N_{z},
\text{ and }
\sum_{i=1}^{N_{z}} \lambda_{i} = 1
\right\}
\end{equation*}](_images/math/78b9a65ebf752b2041242a3b6d84c77e84cecf7d.png)
- represented by a convex polytope (i.e. a unit
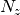 -simplex);
-simplex); - partitioned into
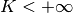 equal-area
equal-area 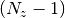 -simplices,
-simplices, 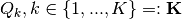 .
.
Relevant functions 
-
simplex_tripart(K)¶ Returns
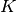 number of equal volume simplex partition elements of unit simplex
number of equal volume simplex partition elements of unit simplex 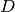 , given by
, given by 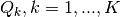 .
.
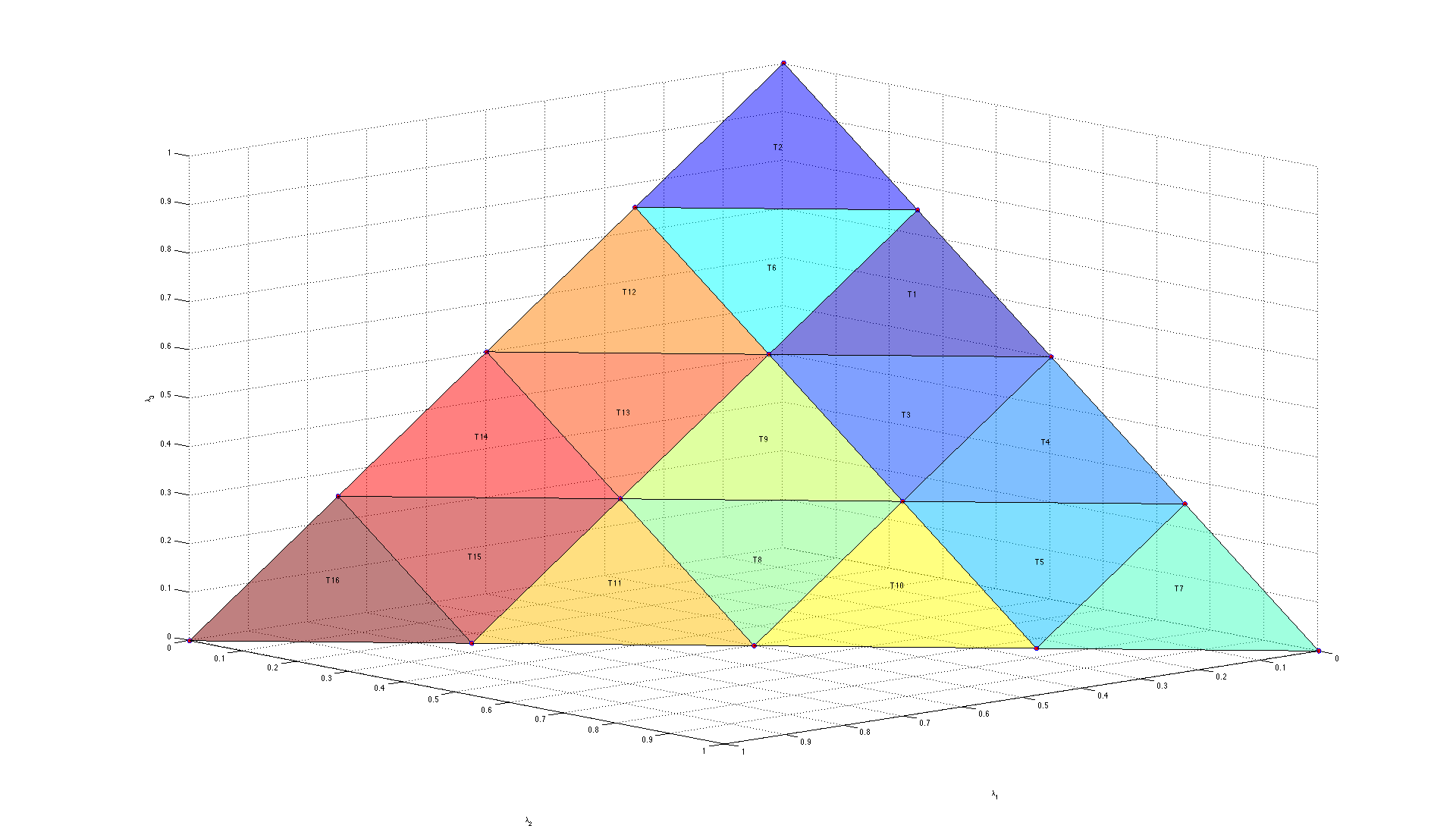
The next figure–Example state-space partition scheme –shows an example where 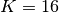 and
and 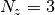 .
.