8. Bilinear programs and SSE operatorΒΆ

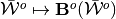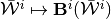Here we give an overview of our main computational insight and proposed method for constructing the operators \bar{\mathcal{W}}^o \mapsto \mathbf{B}^{o}(\bar{\mathcal{W}}^o), and \bar{\mathcal{W}}^i \mapsto \mathbf{B}^{i}(\bar{\mathcal{W}}^i).

Given a candidate correspondence 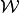\mathcal{W}, evaluating the symmetric sequential equilibrium (SSE) operator at this point in the set of compact and convex-valued correspondences (see Definition 3 in the paper), 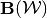\mathbf{B}(\mathcal{W}), will involve:

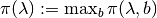  1. Calculating state-dependent max-min punishment values, \pi(\lambda) := \max_{b} \pi(\lambda,b).

    • We show that this is amenable to a separable bilinear program (BLP).
    • We will describe how these BLPs are solved to \epsilon-global optimality.

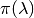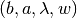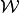  2. Given \pi (\lambda), compute the total-payoff sets supported by action-states-continuation-value tuples, (b,a,\lambda,w), that are admissible with respect to \mathcal{W}:

    • We will show that this consists of subproblems that are non-separable BLPs.
    • These can be solved by a specific stochastic global optimization problem that involves sub-problems that are linear programs (LP).

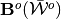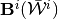We adapt Steps 1 and 2 above for both outer- and inner-approximations, respectively, yielding approximate outer- and inner evaluations of the step-correspondence images \mathbf{B}^{o}(\bar{\mathcal{W}}^{o}) and \mathbf{B}^{i}(\bar{\mathcal{W}}^{i}).