3. Intersections with State-space Partitions¶
For every 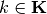 and its associated simplicial partition element
and its associated simplicial partition element 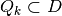 with
positive volume, the
set-valued image
with
positive volume, the
set-valued image 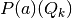 :
:
is another
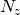 -simplex contained in the unit
-simplex contained in the unit 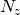 -simplex
-simplex 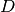 ; and
; andintersects with:
- at least one partition element
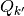 where
where 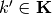 and
and - at most all partition elements
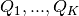 ;
;
- at least one partition element
3.1. Polytope intersection problems¶
Denote
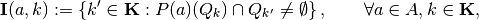
as the sets of indexes to respective partition-elements—i.e. 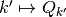 —that contain non-empty
intersections with each simplicial image
—that contain non-empty
intersections with each simplicial image 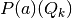 . Each nonempty
intersection, induced by each
. Each nonempty
intersection, induced by each 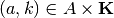 and
and 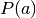 , is described by
, is described by
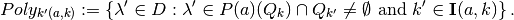
Note
Each intersection 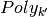 , for each
, for each
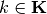 and each
and each 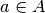 , is a
polytope, and is at least a simplex, and is a subset of partition
element
, is a
polytope, and is at least a simplex, and is a subset of partition
element 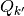 , where
, where 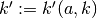 .
.
These nonempty intersections are such that
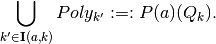
Example
If 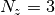 , then
, then 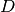 is a unit 2-simplex, and
each
is a unit 2-simplex, and
each 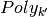 can be a polygon or a triangular subset in
can be a polygon or a triangular subset in 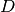 .
.